Seemingly Complex Systems Collapse to Simplicity Without Nonlinearity

In both electrical engineering and artificial intelligence, seemingly complex systems often collapse into simple, manageable forms when nonlinearity is removed. A fascinating analogy exists between Thevenin’s and Norton’s theorems in circuit theory and artificial neural networks (ANNs) without activation functions. While these concepts come from different fields, they share a universal mathematical connection.

What Are Thevenin’s and Norton’s Theorems?

In electrical circuits, Thevenin’s and Norton’s theorems allow us to simplify complicated networks of resistors, voltage sources, and current sources into simpler, equivalent forms:

Thevenin’s Theorem: Any circuit can be replaced by a single voltage source (V_th) in series with a resistance (R_th).

Figure from Wikipedia.

Norton’s Theorem: The same circuit can be replaced by a single current source (I_N) in parallel with a resistance (R_N).

Figure from Wikipedia.

These simplified models behave identically to the original circuits from the perspective of the connection points, making analysis far easier.

Neural Networks Without Activation Functions: A Linear World

Artificial neural networks (ANNs) are typically used to handle complex tasks, such as image recognition or language translation. However, when activation functions are removed, the network becomes a purely linear system:

Each layer applies a linear transformation: y=Wx+b, where W is the weight matrix, x is the input, and b is the bias.
Without nonlinearity, stacking multiple layers simply results in a single equivalent transformation. No matter the number of layers, the entire network can be reduced to one matrix multiplication.

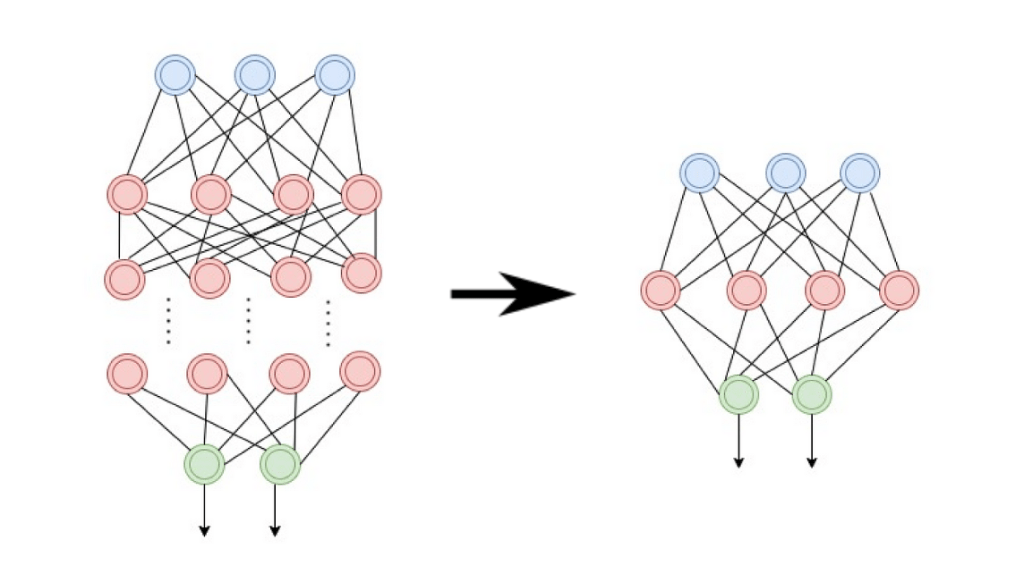
The Mathematical Connection

Both Thevenin’s/Norton’s theorems and linear neural networks leverage the simplicity of linear algebra:

Superposition: Outputs in both cases are directly proportional to inputs. Linear systems allow us to combine multiple effects into a single equivalent representation.
Equivalence: Thevenin’s and Norton’s theorems reduce circuits into their simplest equivalent forms, just as linear ANNs collapse into a single layer.
Matrix Representation: Circuits can be analyzed with impedance or admittance matrices, while linear neural networks are described using weight matrices.

Why Does This Matter?

This analogy reveals a powerful and universal truth: systems that appear complex often collapse into simple equivalents in the absence of nonlinearity. This insight shows how deeply the principles of linearity are embedded in both engineering and AI. By understanding these parallels, we not only simplify problem-solving but also deepen our appreciation for the elegance of mathematics in describing the world.

Sida Liu